Graph representations

 The following two are the most commonly used representations of a graph. 

1. Adjacency Matrix 
2. Adjacency List 

There are other representations also like, Incidence Matrix and Incidence List. The choice of graph representation is situation-specific. It totally depends on the type of operations to be performed and ease of use. 

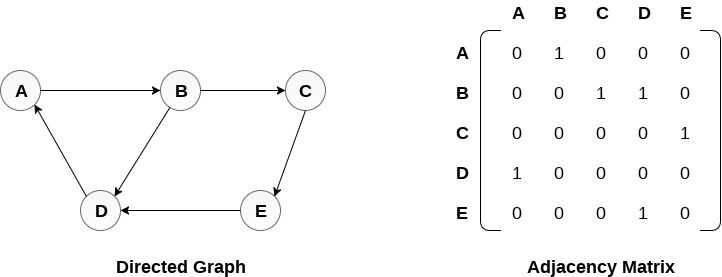
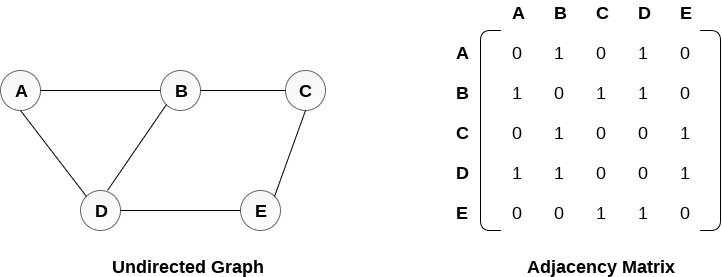
Adjacency Matrix: 
Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w. 

Consider a graph with no. of vertices as V , the adjacency matrix of such a graph is a binary matrix of size V x V. Let us assume the matrix as A , element Aij is 1 if there is an edge from vertex i to vertex j else Aij is 0.

Aij =  1    , if edge exists between i and j

                     0    , otherwise

A directed graph and its adjacency matrix representation is shown in the following figure.

 

An undirected graph and its adjacency matrix representation is shown in the following figure.

Pros: Representation is easier to implement and follow. Removing an edge takes O(1) time. Queries like whether there is an edge from vertex ‘u’ to vertex ‘v’ are efficient and can be done O(1).

Cons: Consumes more space O(V^2). Even if the graph is sparse(contains less number of edges), it consumes the same space. Adding a vertex is O(V^2) time. 

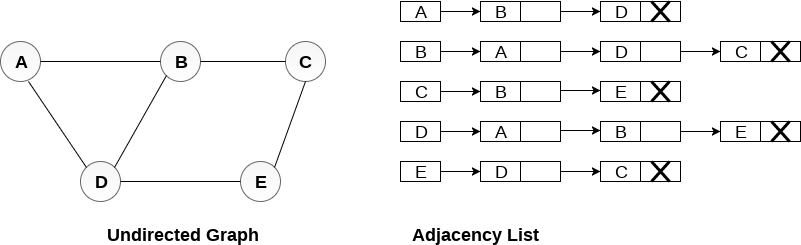
Adjacency List: 
An array of lists is used. The size of the array is equal to the number of vertices. Let the array be an array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. Following is the adjacency list representation of the above graph. 
 

Undirected Graph Adjacency List:

In a directed graph, the sum of lengths of all the adjacency lists is equal to the number of edges present in the graph.

Pros: Saves space O(|V|+|E|) . In the worst case, there can be C(V, 2) number of edges in a graph thus consuming O(V^2) space. Adding a vertex is easier.

Cons: Queries like whether there is an edge from vertex u to vertex v are not efficient and can be done O(V).