Minimum Spanning Tree

 

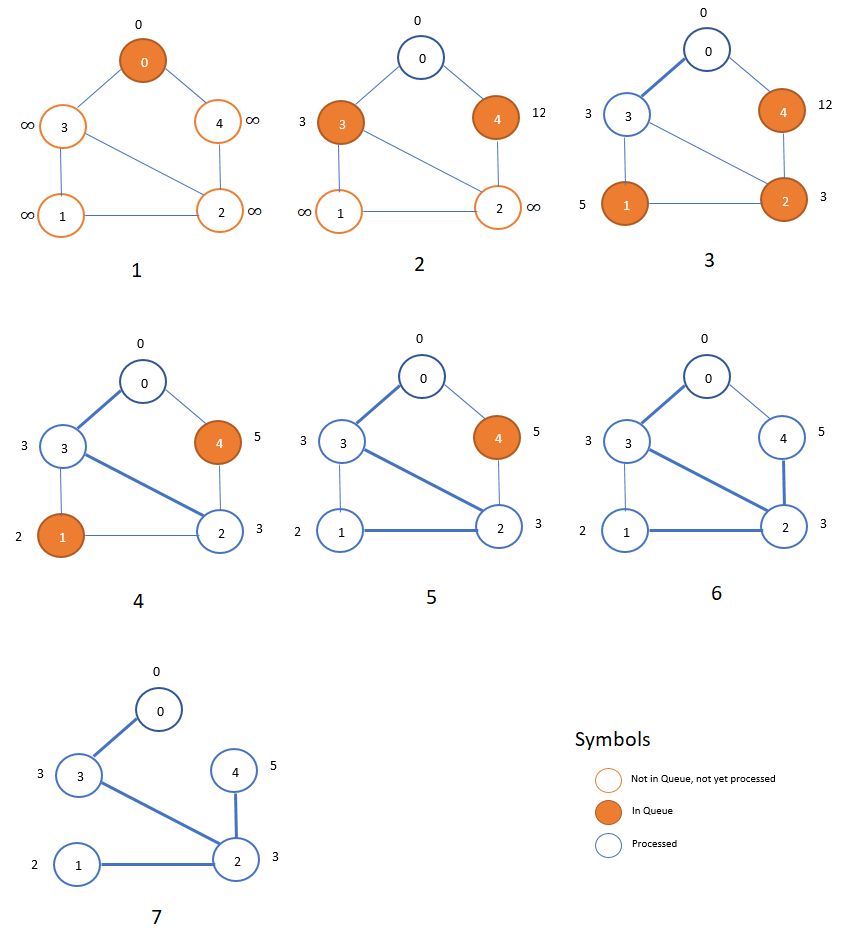
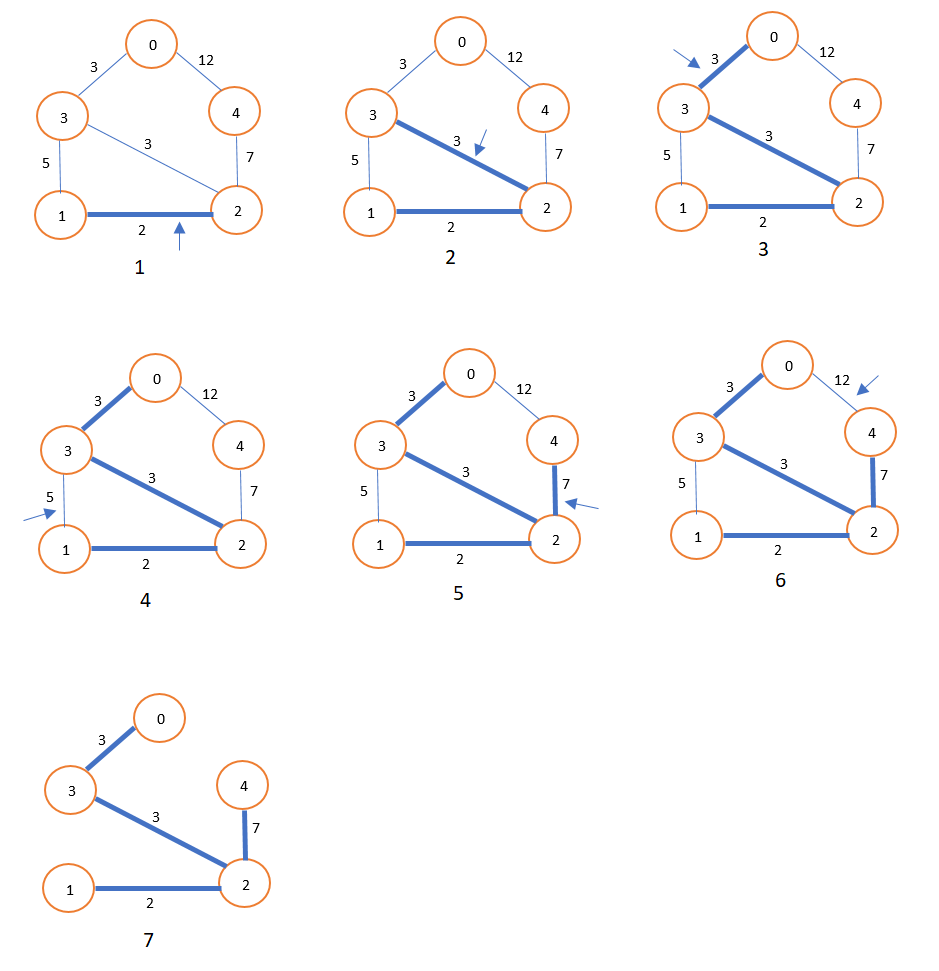
Fig 6. Animation showing a minimum spanning tree (Image by Author)

A minimum spanning tree is a subset of the edges of a graph that connects all the vertices with the minimum sum of edge weights and consists of no cycles.

 A Minimum Spanning Tree (MST) is a sub-set of edges from a graph G={V, E} which connects all the vertices together. A graph may have multiple spanning trees but a minimum spanning tree has least sum of weight in all possible spanning trees. If there are V vertices in MST then only V-1 edges can be present

Figure 6 is an animation showing the process of obtaining a minimum spanning tree.

Algorithms

1.    Prim’s algorithm

2.   Kruskal’s algorithm

Applications

·        Used to construct trees for broadcasting in computer networks.

·        Used in graph-based cluster analysis.

·        Used in image segmentation.

·        Used in regionalisation of socio-geographic areas, where regions are grouped into contiguous regions.

 

1.Prim’s Algorithm:

Ø Create a set that keeps track of vertices already included in MST. 

Ø Assign a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign key value as 0 for the first vertex so that it is picked first. 

Ø While set doesn’t include all vertices 

§  Pick a vertex u which is not there in set and has minimum key                        value.

§  Include u to set. 

§  Update key value of all adjacent vertices of u. To update the key         values, iterate through all adjacent vertices. For every adjacent          vertex v, if weight of edge u-v is less than the previous key value of v, update the key value as weight of u-v

Kruskals Algorithm:

The algorithm starts with V different trees (V is the vertices in the graph).

Every time Kruskal’s alorithm selects an edge that has minimum weight and then adds that edge if it doesn’t create a cycle.

When the algorithm is completed, there will be only one tree, and that is the minimum spanning tree.

There are two ways of implementing Kruskal’s algorithm:

• By using Disjoint Sets: Using UNION and FIND operations

• By using Priority Queues: Maintains weights in priority queue

The appropriate data structure is the UNION/FIND algorithm [for implementing forests]. Two vertices belong to the sam
e set if and only if they are connected in the current spanning forest.

Each vertex is initially in its own set. If u and v are in the same set, the edge is rejected because it forms a cycle. Otherwise, the edge is accepted, and a UNION is performed on the two sets containing u and v.