Shortest Path

 

Figure shows an animation where the shortest path is determined from vertex 1 to vertex 6 in a graph.

The shortest path from one vertex to another vertex is a path in the graph such that the sum of the weights of the edges that should be travelled is minimum.

The shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized.The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs, where the vertices correspond to intersections and the edges correspond to road segments, each weighted by the length of the segment.

Algorithms

1.    Dijkstra’s shortest path algorithm

Pseudocode

Dijkstra’s shortest path algorithm:

Algorithm:

1. Mark all nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
2. Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes. Set the initial node as current.
3. For the current node, consider all of its unvisited neighbors and calculate their tentative distances through the current node. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one. When we are done considering all of the unvisited neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again.
4. If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
5. Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new "current node", and go back to step 3.

Dijkstra’s Algorithm:

 

Pseudocode:

 1  function Dijkstra(Graph, source):
 2
 3      create vertex set Q
 4
 5      for each vertex v in Graph:            
 6          dist[v] ← INFINITY                 
 7          prev[v] ← UNDEFINED                
 8          add v to Q                     
 9      dist[source] ← 0                       
10     
11      while Q is not empty:
12          u ← vertex in Q with min dist[u]   
13                                             
14          remove u from Q
15         
16          for each neighbor v of u:           // only v that are still in Q
17              alt ← dist[u] + length(u, v)
18              if alt < dist[v]:              
19                  dist[v] ← alt
20                  prev[v] ← u
21 

22 return dist[], prev[] 

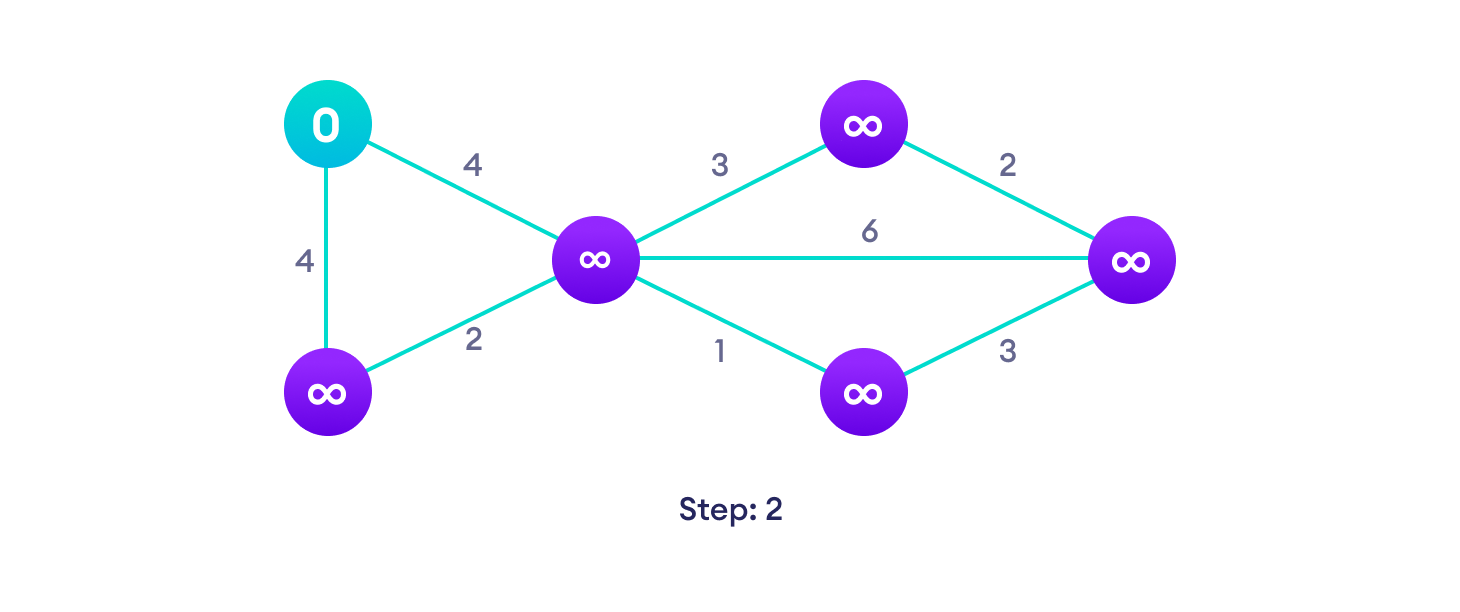
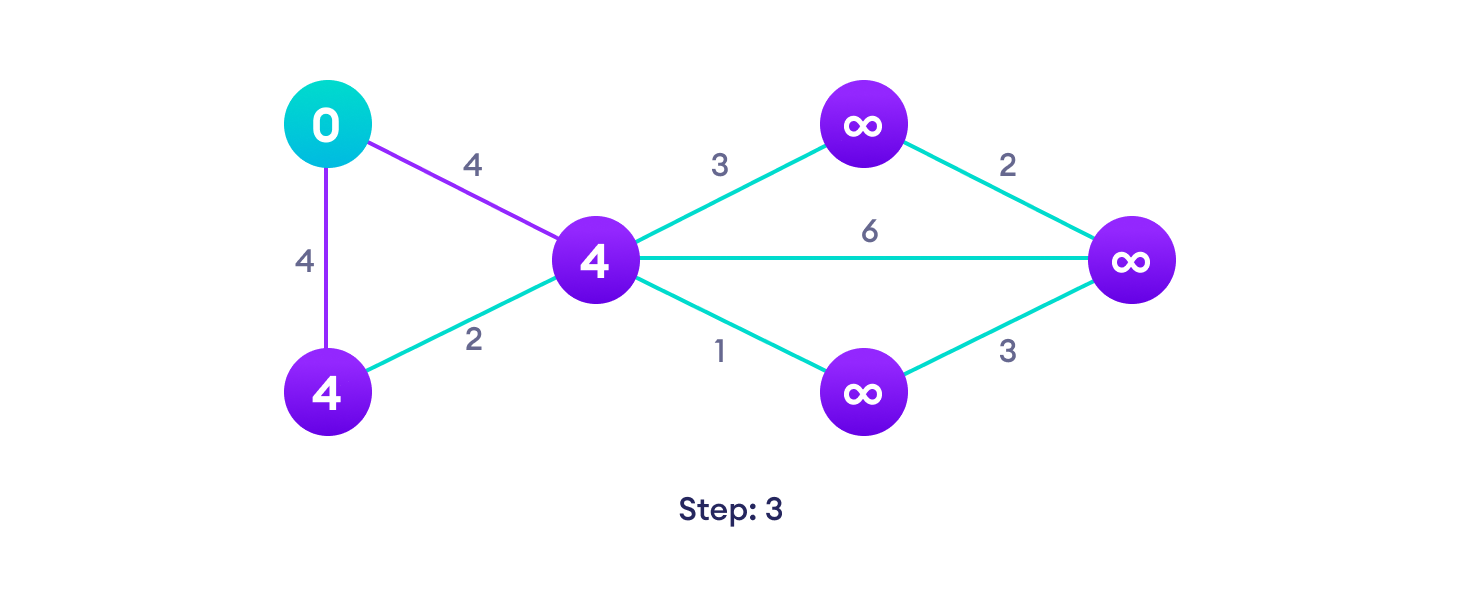
Example of Dijkstra's algorithm

It is easier to start with an example and then think about the algorithm.

Start with a weighted graph

Choose a starting vertex and assign infinity path values to all other devices

Go to each vertex and update its path length

If the path length of the adjacent vertex is lesser than new path length, don't update it

Avoid updating path lengths of already visited vertices

After each iteration, we pick the unvisited vertex with the least path length. 

So we choose 5 before 7

Notice how the rightmost vertex has its path length updated twice

Applications

·        Used to find directions to travel from one location to another in mapping software like Google maps or Apple maps.

·        Used in networking to solve the min-delay path problem.

·        Used in abstract machines to determine the choices to reach a certain goal state via transitioning among different states (e.g., can be used to determine the minimum possible number of moves to win a game)