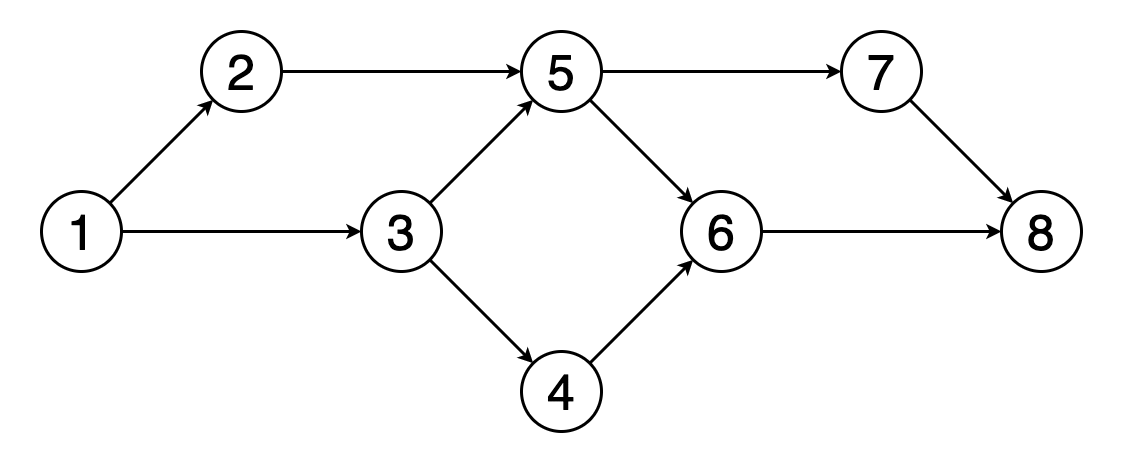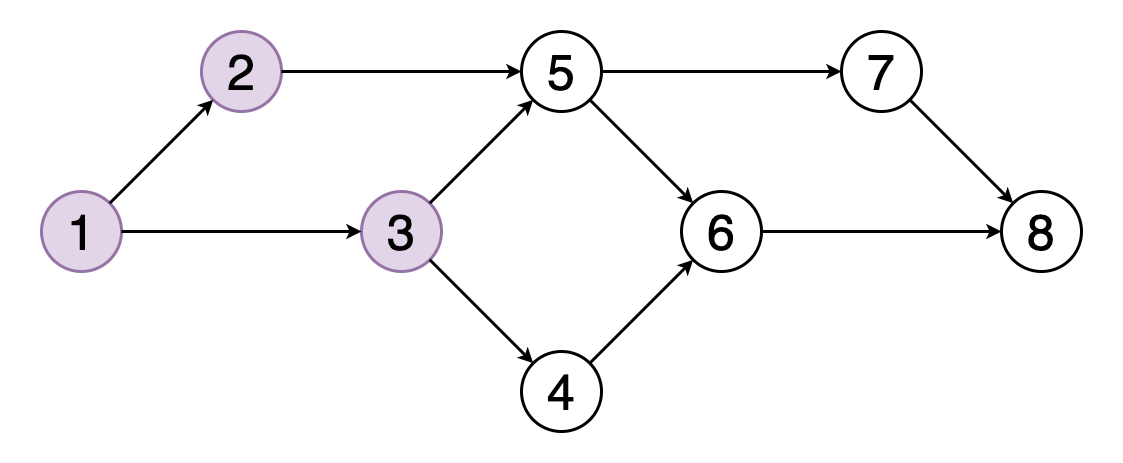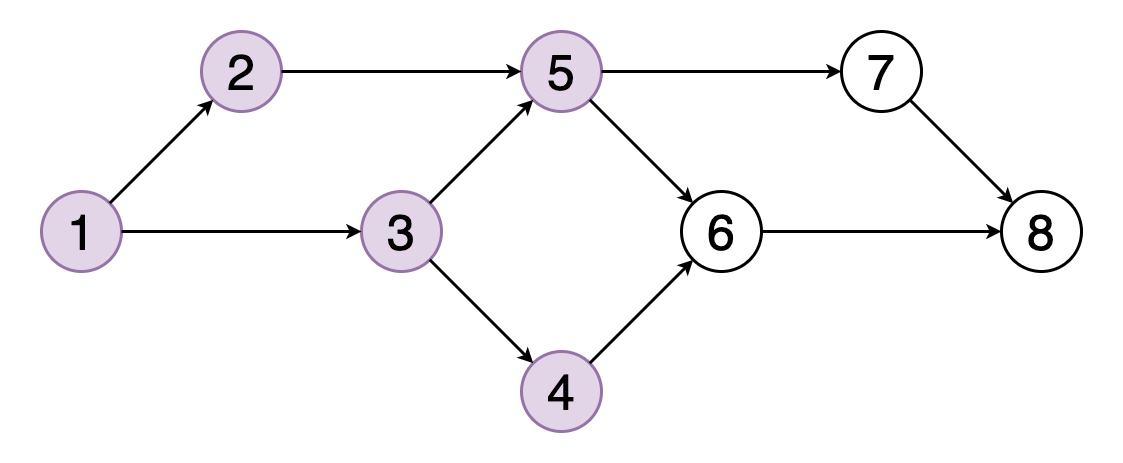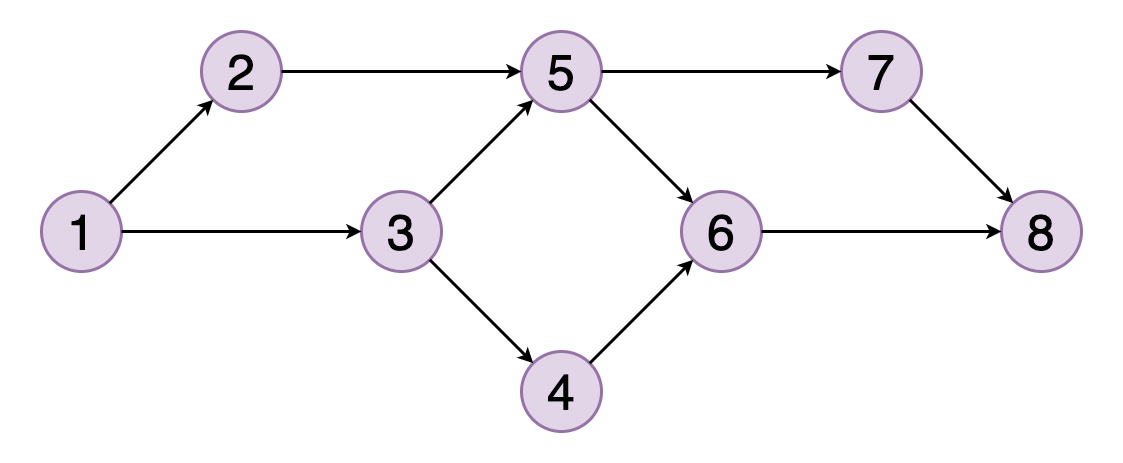
Topological Sorting

 

Topological sorting of a graph is a linear ordering of its vertices so that for each directed edge (u, v) in the ordering, vertex u comes before v.

Figure shows an example of a topological ordering of vertices (1, 2, 3, 5, 4, 6, 7, 8). You can see that vertex 5 should come after vertices 2 and 3. Similarly, vertex 6 should come after vertices 4 and 5.

Steps

1. Topological sort is an ordering of vertices in a directed acyclic graph [DAG] in which each node comes before all nodes to which it has outgoing edges.
2. Indegree is computed for all vertices, starting with the vertices which are having indegree 0. 
3. Queue can be used to keep track of vertices with indegree zero. While the queue is not empty, a vertex is removed, and all edges adjacent to it have their indegrees decremented.
4. Topological sorting for a graph is not possible if graph is not DAG.
5. If a Hamiltonian path exists, the topological sort order is unique. If a topological sort does not form a Hamiltonian path, DAG can have two or more topological orderings.

Applications

• Used in instruction scheduling.
• Used in data serialisation.
• Used to determine the order of compilation tasks to perform in makefiles.
• Used to resolve symbol dependencies in linkers.