What are Graphs?

on



 


Definition:

A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links.  More formally a Graph can be defined as

A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes.



Graphs are used to solve many real-life problems. Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks.

Properties:

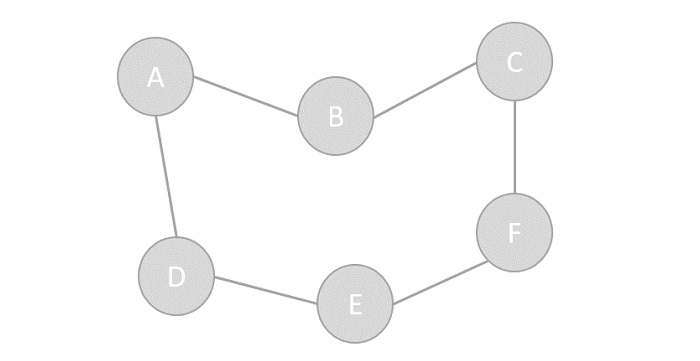
  • Vertex − Each node of the graph is represented as a vertex. 

  • Edge − Edge represents a path between two vertices or a line between two vertices. In the figure there's the lines from A to B, B to C, and so on represents edges

  • Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the figure example, B is adjacent to A, C is adjacent to B, and so on.

  • Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.

Types of nodes

  • Root node: The root node is the ancestor of all other nodes in a graph. It does not have any ancestor. Each graph consists of exactly one root node. Generally, you must start traversing a graph from the root node.

  • Leaf nodes: In a graph, leaf nodes represent the nodes that do not have any successors. These nodes only have ancestor nodes. They can have any number of incoming edges but they will not have any outgoing edges.

Types of graphs

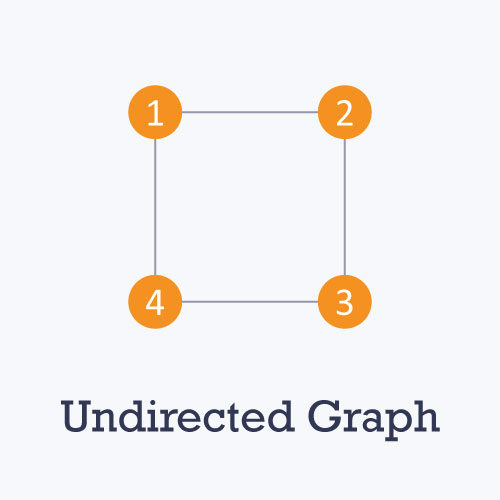
  • Undirected: An undirected graph is a graph in which all the edges are bi-directional i.e. the edges do not point in any specific direction.

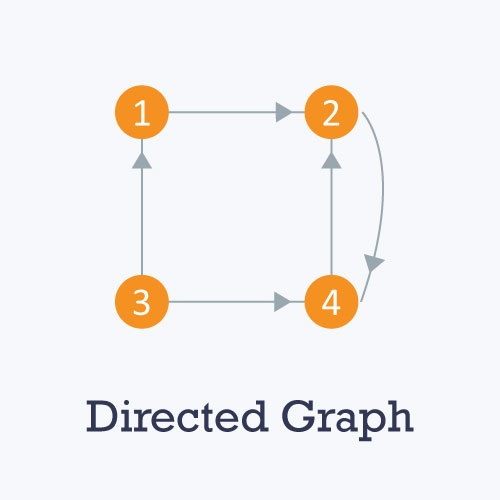
enter image description here

  • Directed: A directed graph is a graph in which all the edges are uni-directional i.e. the edges point in a single direction.

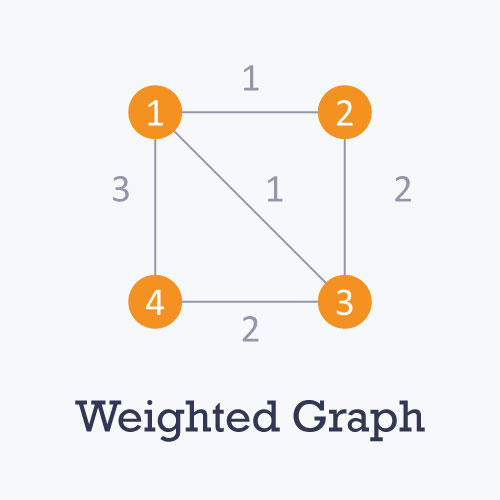
enter image description here

  • Weighted: In a weighted graph, each edge is assigned a weight or cost.

enter image description here

  • Cyclic: A graph is cyclic if the graph comprises a path that starts from a vertex and ends at the same vertex. That path is called a cycle. An acyclic graph is a graph that has no cycle.

Need of Graph Data structures:

  • Can represent many real world problems

  • Represent/Store data in non linear way

  • They are extremely useful for comparing values in different categories and can be used to describe the relationship of several variables at once

Comments

Post a Comment